题目内容
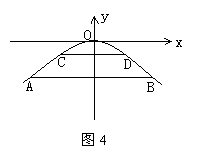
如图1,有一座抛物线型拱桥,涨潮时桥内水面宽AB为8米,落潮时水位下降5米,桥内水面宽CD为12米.

(1)建立适当的平面直角坐标系,并求此抛物线的解析式;
(2)如图2,某种货船在水面上的部分的横截面是梯形EFGH,且HE=FG,EF=
HE,∠GHE=45°.试问落潮时,能顺利通过拱桥的这种货船在水面上的部分最大高度是多少?

(1)建立适当的平面直角坐标系,并求此抛物线的解析式;
(2)如图2,某种货船在水面上的部分的横截面是梯形EFGH,且HE=FG,EF=
| 2 |
分析:(1)可以CD所在的直线为x轴,线段CD的中点为坐标原点,CD的垂直平分线为y轴,建立平面直角坐标系,则此抛物线的对称轴为y轴,故可设抛物线的解析式为:y=ax2+c,再将B(4,5),D(6,0)代入,运用待定系数法即可求出此抛物线的解析式;
(2)落潮时,水位在CD,此时EF落在CD上,如图,过点作EM⊥HG于点M,求出EM即可.设EM=h,则可用含h的代数式G点的坐标为(2h,h),然后把G点的坐标代入(1)中所求的解析式y=-
x2+9中,得到关于h的方程,求解即可.
(2)落潮时,水位在CD,此时EF落在CD上,如图,过点作EM⊥HG于点M,求出EM即可.设EM=h,则可用含h的代数式G点的坐标为(2h,h),然后把G点的坐标代入(1)中所求的解析式y=-
| 1 |
| 4 |
解答: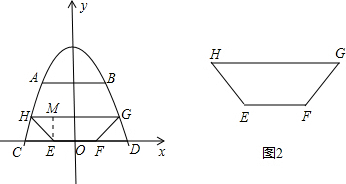 解:(1)以CD所在的直线为x轴,线段CD的中点为坐标原点,CD的垂直平分线为y轴,建立如图所示的平面直角坐标系.
解:(1)以CD所在的直线为x轴,线段CD的中点为坐标原点,CD的垂直平分线为y轴,建立如图所示的平面直角坐标系.
∵AB为8米,落潮时水位下降5米,桥内水面宽CD为12米.
∴B(4,5),D(6,0).
抛物线的解析式可设为:y=ax2+c.
由题意得:
,
解得
,
∴y=-
x2+9;
(2)过点作EM⊥HG于点M.
∵∠GHE=45°,∴EM=HM.
设EM=HM=h,则EH=
HM,
∴EF=
EH=2HM=2h,
∴G(2h,h),
∴h═-
(2h)2+9,
解得:h1=
,h2=
(不合题意,舍去)
故落潮时,能顺利通过拱桥的这种货船在水面上的部分最大高度是
米.
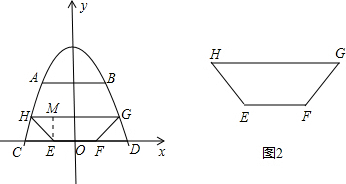 解:(1)以CD所在的直线为x轴,线段CD的中点为坐标原点,CD的垂直平分线为y轴,建立如图所示的平面直角坐标系.
解:(1)以CD所在的直线为x轴,线段CD的中点为坐标原点,CD的垂直平分线为y轴,建立如图所示的平面直角坐标系.∵AB为8米,落潮时水位下降5米,桥内水面宽CD为12米.
∴B(4,5),D(6,0).
抛物线的解析式可设为:y=ax2+c.
由题意得:
|
解得
|
∴y=-
| 1 |
| 4 |
(2)过点作EM⊥HG于点M.
∵∠GHE=45°,∴EM=HM.
设EM=HM=h,则EH=
| 2 |
∴EF=
| 2 |
∴G(2h,h),
∴h═-
| 1 |
| 4 |
解得:h1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
故落潮时,能顺利通过拱桥的这种货船在水面上的部分最大高度是
-1+
| ||
| 2 |
点评:本题考查了运用待定系数法求二次函数的解析式及二次函数的应用,难度中等.注意(1)中如果选取不同的坐标系,那么求得的解析式也不同,本问答案不唯一;(2)中设出EM=h,则用含h的代数式表示G点的坐标是解题的关键.

练习册系列答案
相关题目
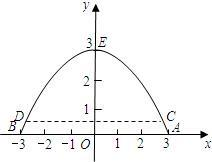 度是多少米?
度是多少米? 如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( )
如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( )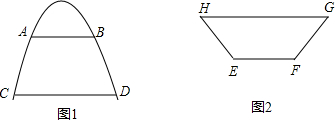
 HE,∠GHE=45°.试问落潮时,能顺利通过拱桥的这种货船在水面上的部分最大高度是多少?
HE,∠GHE=45°.试问落潮时,能顺利通过拱桥的这种货船在水面上的部分最大高度是多少?