Question

【题目】如图，△ABC和△A′B′C′关于直线对称，下列结论中：①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）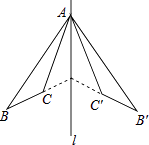

A.4个
B.3个
C.2个
D.1个

Answer 1

【答案】B
【解析】∵△ABC和△A′B′C′关于直线l对称，∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC，正确；
②l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误。
综上所述，结论正确的是①②③共3个。
故答案为：B
轴对称的性质：关于某条直线对称的两个图形是全等形；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。根据性质可知④不符合题意，其余三个都符合题意。