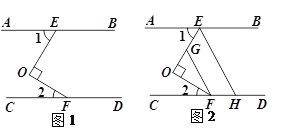题目内容
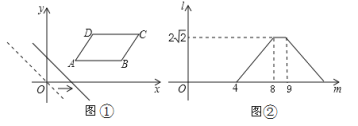
【题目】如图①,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示,那么AD的长为__________.
【答案】![]()
【解析】
根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是8时,直线经过D,在移动距离是9时经过B,得到AB=9-4=5, ![]() , 作DM⊥AB于点M,求出MN的值,再根据勾股定理即可得到答案;
, 作DM⊥AB于点M,求出MN的值,再根据勾股定理即可得到答案;
解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是8时,直线经过D,在移动距离是9时经过B,
则AB=9-4=5,
如图1,当直线经过D点,设交AB与N,则![]() , 作DM⊥AB于点M.
, 作DM⊥AB于点M.

∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DNM=45°,
∴![]() ,
,
∴![]() ,
,
![]() (勾股定理);
(勾股定理);

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】为了保护环境,某企业决定购买10台污水处理设备;现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
处理污水量(吨/月) | 240 | 200 |
年消耗费(万元/台) | 1 | 1 |
经预算,该企业购买设备的资金不高于105万元。
(1) 请你设计该企业有几种购买方案;
(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?