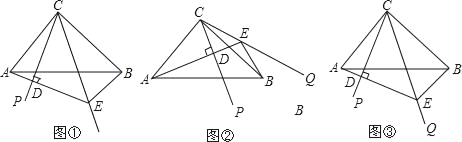
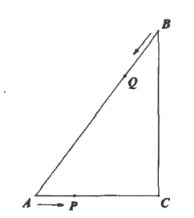
��Ŀ����
����Ŀ����֪�������ϣ�һ����![]() ��ԭ��
��ԭ��![]() ��������ֱ����ÿ����
��������ֱ����ÿ����![]() ����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�
����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ������
���������
![]()
��1�����![]() ���Ӻ�
���Ӻ�![]() ������λ�ã�
������λ�ã�
��2������������ϻ���һ������![]() ����
����![]() ��ԭ��
��ԭ��![]() ���20����λ���ȣ��ʣ�����
���20����λ���ȣ��ʣ�����![]() ��ԭ��������������
��ԭ��������������![]() �غ������ܣ����һ�����
�غ������ܣ����һ�����![]() �غ���ʱ�䣿�����ܣ���˵�����ɣ�
�غ���ʱ�䣿�����ܣ���˵�����ɣ�
���𰸡���1��Q���ک�2����2���ٵ���A��ԭ�����ʱ��ʱ��=390�루6.5���ӣ����ڵ���Aԭ�����ʱ��ʱ��=410�� ��6![]() ���ӣ���
���ӣ���
��������
��1���ȸ���·��=�ٶ���ʱ�����5�����߹���·�̣�Ȼ���������Ҽ���ʽ���㼴�ɵý⣻
��2���ֵ�A��ԭ��������ұ���������ֱ���������߹���·�̣�Ȼ�����ʱ��=·�����ٶȼ��㼴�ɵý⣮
�⣺��1����2��5=10��
����Q�߹���·����1+2+3+4=10��Q���ڣ�1��2+3��4=4��6=��2��
��2��������A��ԭ�����ʱ������Ҫ��n�ε����A����![]() =20�����n=39��
=20�����n=39��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+|��38|+39��
=1+2+3+��+39��
=![]() =780��
=780��
��ʱ��=780��2=390�루6.5���ӣ���
������Aԭ�����ʱ������Ҫ��n�ε����A����![]() =20��
=20��
���n=40��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+39+|��40|��
=1+2+3+��+40��
=![]() =820��
=820��
��ʱ��=820��2=410�� ��6![]() ���ӣ���
���ӣ���

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�