题目内容
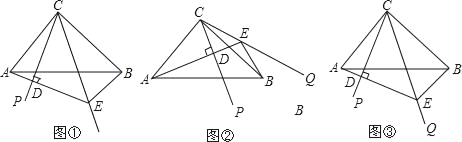
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
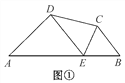
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
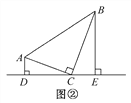
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.
【答案】(1)见解析 (2)AD=BE+DE (3)8
【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;
(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;
(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.
试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
故答案为:AD=BE+DE.
(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD=![]() ×6=2,∴AE=AD+DE=2+6=8.
×6=2,∴AE=AD+DE=2+6=8.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
体温 | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
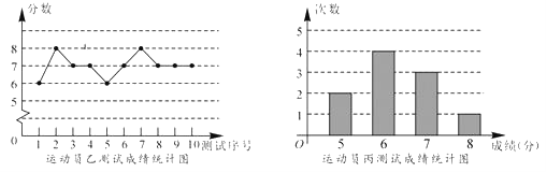
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)