题目内容
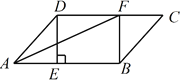
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)32
【解析】
(1)先求出四边形BFDE是平行四边形,再根据矩形的判定推出即可;
(2)根据勾股定理求出DE长,即可得出答案.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵AF平分∠DAB,
∴∠DAF=∠FAB,
∵平行四边形ABCD,
∴AB∥CD,
∴∠FAB=∠DFA,
∴∠DFA=∠DAF,
∴AD=DF=5,
在Rt△ADE中,DE=![]() ,
,
∴平行四边形ABCD的面积=ABDE=4×8=32,

练习册系列答案
相关题目