题目内容
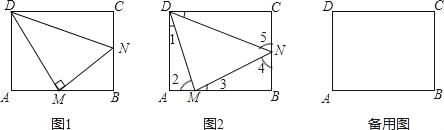
【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
【答案】(1)见解析:(2)2![]() .
.
【解析】
(1)证明△ABP≌△BCQ,则∠PAB=∠CBQ,从而证明∠PAB+∠ABQ=90°,进而得证;
(2)由折叠的性质可得∠BQE=∠C=90°,∠QBE=∠QBC,再根据EQ=EF,可得BE垂直平分FQ,从而有BF=BQ,进而可得∠FBE=∠EBQ,再根据∠FBE+∠EBQ+∠QBC=∠ABC=90°,求出∠QBC=30°,可得BQ=2CQ,在Rt△BCQ中,利用勾股定理求出CQ长即可求得答案.
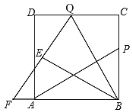
(1)AP=BQ,AP⊥BQ,证明如下:
∵ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC,
又∵BP=CQ,
∴△ABP≌△BCQ(SAS),
∴AP=BQ,∠PAB=∠CBQ,
∵∠CBQ+∠ABQ=∠ABC=90°,
∴∠PAB+∠ABQ=90°,
∴∠AMB=90°,
∴AP⊥BQ;
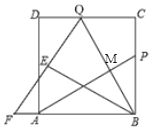
(2)∵将△BQC沿BQ所在的直线翻折得到△BQE,
∴∠BQE=∠C=90°,∠QBE=∠QBC,
又∵EQ=EF,
∴BE垂直平分FQ,
∴BF=BQ,
∴∠FBE=∠EBQ,
∵∠FBE+∠EBQ+∠QBC=∠ABC=90°,
∴∠QBC=30°,
∴BQ=2CQ,
在Rt△BCQ中,BQ2=BC2+CQ2,即(2CQ)2=62+CQ2,
∴CQ=2![]() ,
,
∵BP=CQ,
∴BP=2![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目