题目内容
【题目】⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
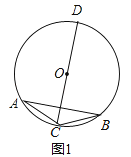
(1)如图1,AC=BC
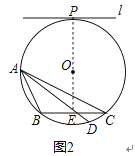
(2)如图2,直线l与⊙O相切于点P,且l∥BC。
【答案】
(1)
解:如图1,
直径CD为所求;
(2)
解:如图2,
弦AD为所求.
【解析】(1)过点C作直径CD,由于AC=BC,![]() ,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;
,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;
(2)连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.
此题考查了圆的应用,根据垂径定理,切线的性质即可解答问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
(2)根据(1)中所画图象,完成下列表格:
两人相遇次数 | 1 | 2 | 3 | 4 | … | n |
两人所跑路程之和 | 100 | 300 | … |
|
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.










