题目内容
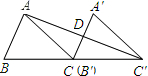 已知△ABC的面积为36,将△ABC沿BC平移到△A′B′C′,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为
已知△ABC的面积为36,将△ABC沿BC平移到△A′B′C′,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为分析:根据平移变换只改变图形的位置,不改变图形的形状与大小,可得∠B=∠A′CC′,BC=B′C′,再根据同位角相等,两直线平行可得CD∥AB,然后求出CD=
AB,点C′到A′C的距离等于点C到AB的距离,根据等高的三角形的面积的比等于底边的比即可求解.
| 1 |
| 2 |
解答:解:根据题意得,∠B=∠A′CC′,BC=B′C′,
∴CD∥AB,CD=
AB(三角形的中位线),
∵点C′到A′C的距离等于点C到AB的距离,
∴△C′DC的面积=
△ABC的面积=
×36=18.
故答案为:18.
∴CD∥AB,CD=
| 1 |
| 2 |
∵点C′到A′C的距离等于点C到AB的距离,
∴△C′DC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:18.
点评:本题考查了平移变换的性质,平行线的判定与性质,三角形的中位线等于第三边的一半的性质,以及等高三角形的面积的比等于底边的比,是小综合题,但难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
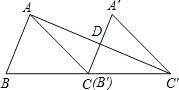 已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( ) 25、如图,已知△ABC的面积为3,且AE=AC,现将△ABC沿CA方向平移CA长度得到△EFA,求四边形CEFB的面积.
25、如图,已知△ABC的面积为3,且AE=AC,现将△ABC沿CA方向平移CA长度得到△EFA,求四边形CEFB的面积.