题目内容
如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,已知△ABC的面积为1,按此规律,则△AnBnCn的面积是
.

| 1 |
| 22n |
| 1 |
| 22n |

分析:由于A1、B1、C1分别是△ABC的边BC、CA、AB的中点,就可以得出△A1B1C1∽△ABC,且相似比为
,就可求出S△A1B1C1=
,同样地方法得出S△A2B2C2=
,S△A3B3C3=
…所以就可以求出S△AnBnCn的值.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 64 |
解答:解:∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点,
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
∴S△A1B1C1:S△ABC=1:4,且S△ABC=1
∴S△A1B1C1=
.
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A1B1C1的∽△A2B2C2且相似比为
∴S△A2B2C2=
.依此类推
∴S△A3B3C3=
…
∴S△AnBnCn=
.
故答案为:
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
| 1 |
| 2 |
∴S△A1B1C1:S△ABC=1:4,且S△ABC=1
∴S△A1B1C1=
| 1 |
| 4 |
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A1B1C1的∽△A2B2C2且相似比为
| 1 |
| 2 |
∴S△A2B2C2=
| 1 |
| 16 |
∴S△A3B3C3=
| 1 |
| 64 |
∴S△AnBnCn=
| 1 |
| 22n |
故答案为:
| 1 |
| 22n |
点评:本题考查了三角形中位线定理的运用,相似三角形的判定与性质的运用.

练习册系列答案
相关题目

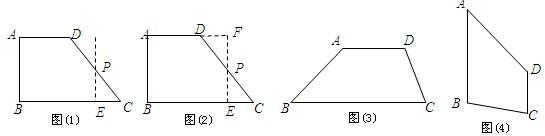
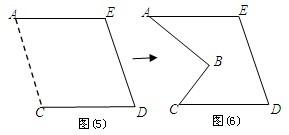
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,在Rt∠ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,在Rt∠ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
 x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.