题目内容
直线y=- x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A
x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A 点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.(1)直接写出A、B两点的坐标;
(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;
(3)当S=
 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
【答案】分析:(1)分别令y=0,x=0,即可求出A、B的坐标;
(2)因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A的时间是8秒,点P的速度是2,从而可求出,
当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得 ,利用S=
,利用S= OQ×PD,即可求出答案;
OQ×PD,即可求出答案;
(3)令S= ,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.
,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.
解答: 解:(1)y=0,x=0,求得A(8,0),B(0,6),
解:(1)y=0,x=0,求得A(8,0),B(0,6),
(2)∵OA=8,OB=6,
∴AB=10.
∵点Q由O到A的时间是 (秒),
(秒),
∴点P的速度是 =2(单位长度/秒).
=2(单位长度/秒).
当P在线段OB上运动(或O≤t≤3)时,
OQ=t,OP=2t,S=t2.
当P在线段BA上运动(或3<t≤8)时,
OQ=t,AP=6+10-2t=16-2t,
如图,过点P作PD⊥OA于点D,
由 ,得PD=
,得PD= .
.
∴S= OQ•PD=-
OQ•PD=- .
.
(3)当S= 时,∵
时,∵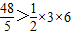 ,∴点P在AB上
,∴点P在AB上
当S= 时,-
时,- =
=
∴t=4
∴PD= =
= ,AP=16-2×4=8
,AP=16-2×4=8
AD= =
=
∴OD=8- =
=
∴P( ,
, )
)
M1( ,
, ),M2(-
),M2(- ,
, ),M3(
),M3( ,-
,- )
)
点评:本题需仔细分析题意,结合图象,利用函数解析式即可解决问题.
(2)因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A的时间是8秒,点P的速度是2,从而可求出,
当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得
 ,利用S=
,利用S= OQ×PD,即可求出答案;
OQ×PD,即可求出答案;(3)令S=
 ,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.
,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:
 解:(1)y=0,x=0,求得A(8,0),B(0,6),
解:(1)y=0,x=0,求得A(8,0),B(0,6),(2)∵OA=8,OB=6,
∴AB=10.
∵点Q由O到A的时间是
 (秒),
(秒),∴点P的速度是
 =2(单位长度/秒).
=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,
OQ=t,OP=2t,S=t2.
当P在线段BA上运动(或3<t≤8)时,
OQ=t,AP=6+10-2t=16-2t,
如图,过点P作PD⊥OA于点D,
由
 ,得PD=
,得PD= .
.∴S=
 OQ•PD=-
OQ•PD=- .
.(3)当S=
 时,∵
时,∵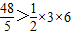 ,∴点P在AB上
,∴点P在AB上当S=
 时,-
时,- =
=
∴t=4
∴PD=
 =
= ,AP=16-2×4=8
,AP=16-2×4=8AD=
 =
=
∴OD=8-
 =
=
∴P(
 ,
, )
)M1(
 ,
, ),M2(-
),M2(- ,
, ),M3(
),M3( ,-
,- )
)点评:本题需仔细分析题意,结合图象,利用函数解析式即可解决问题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
表1给出了直线l1上部分点(x,y)的坐标值,表2给出了直线l2上部分点(x,y)的坐标值.
表1:
| x | -2 | 0 | 2 | 4 |
| y | 3 | 1 | -1 | -3 |
| x | -2 | 0 | 2 |
| y | -5 | -3 | -1 |
(2)直线l1、l2与y轴围成的三角形的面积等于______.
 (2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
(2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.
如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.