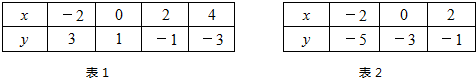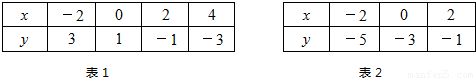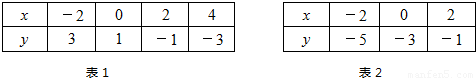题目内容
表1给出了直线l1上部分点(x,y)的坐标值,表2给出了直线l2上部分点(x,y)的坐标值.
表1:
| x | -2 | 0 | 2 | 4 |
| y | 3 | 1 | -1 | -3 |
| x | -2 | 0 | 2 |
| y | -5 | -3 | -1 |
(2)直线l1、l2与y轴围成的三角形的面积等于______.
解:(1)由表1可知,当x=0时,y=1,
所以,直线l1与y轴的交点坐标是(0,1);
(2)由表2可知,当x=0时,y=-3,
所以,直线l2与y轴的交点坐标(0,-3),
∵两直线x=2时,y=-1,
∴两直线的交点坐标为(2,-1),
∴直线l1、l2与y轴围成的三角形的面积= [1-(-3)]×2=4.
[1-(-3)]×2=4.
故答案为:(0,1),4.
分析:(1)根据y轴上的点的横坐标为0解答即可;
(2)根据表2得到直线l2与y轴的交点坐标,以及两直线的交点坐标,然后根据三角形的面积公式列式进行计算即可得解.
点评:本题考查了两直线相交的问题,仔细观察图表数据,判断出两直线与y轴的交点以及两直线的交点坐标是解题的关键.
所以,直线l1与y轴的交点坐标是(0,1);
(2)由表2可知,当x=0时,y=-3,
所以,直线l2与y轴的交点坐标(0,-3),
∵两直线x=2时,y=-1,
∴两直线的交点坐标为(2,-1),
∴直线l1、l2与y轴围成的三角形的面积=
 [1-(-3)]×2=4.
[1-(-3)]×2=4.故答案为:(0,1),4.
分析:(1)根据y轴上的点的横坐标为0解答即可;
(2)根据表2得到直线l2与y轴的交点坐标,以及两直线的交点坐标,然后根据三角形的面积公式列式进行计算即可得解.
点评:本题考查了两直线相交的问题,仔细观察图表数据,判断出两直线与y轴的交点以及两直线的交点坐标是解题的关键.

练习册系列答案
相关题目