题目内容
 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.
如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.(1)求点A、B、Q的坐标,
(2)若点P在坐x轴上,且PO=24,求△APQ的面积.
分析:(1)首先求出A,B点坐标,再利用直线AB上有一点Q在第一象限且到y轴的距离为2,得出点Q的横坐标为2,即可得出Q点坐标;
(2)根据当点P在x轴的正半轴上时,当点P′在x轴的负半轴上时分别求出即可.
(2)根据当点P在x轴的正半轴上时,当点P′在x轴的负半轴上时分别求出即可.
解答: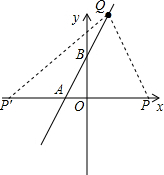 解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,
解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,
∴y=0时,x=-2,x=0时,y=4,故A(-2,0),B(0,4),
由直线AB上有一点Q在第一象限且到y轴的距离为2.
得点Q的横坐标为2,此时y=4+4=8,
所以:Q(2,8);
(2)由A(-2,0)得OA=2
由Q(2,8)可得△APQ中AP边上的高为8,
当点P在x轴的正半轴上时,AP=OA+PO=2+24=26,
S△APQ=
×26×8=104;
当点P′在x轴的负半轴上时,AP′=P′O-OA=24-2=22,
S△AP′Q=
×22×8=88.
 解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,
解:(1)∵直线y=2x+4与x轴交于点A,与y轴交于点B,∴y=0时,x=-2,x=0时,y=4,故A(-2,0),B(0,4),
由直线AB上有一点Q在第一象限且到y轴的距离为2.
得点Q的横坐标为2,此时y=4+4=8,
所以:Q(2,8);
(2)由A(-2,0)得OA=2
由Q(2,8)可得△APQ中AP边上的高为8,
当点P在x轴的正半轴上时,AP=OA+PO=2+24=26,
S△APQ=
| 1 |
| 2 |
当点P′在x轴的负半轴上时,AP′=P′O-OA=24-2=22,
S△AP′Q=
| 1 |
| 2 |
点评:此题主要考查了一次函数图象上点的特征以及三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )