题目内容
过⊙O内一点M的最长弦长为10cm，最短弦长为8cm，那么OM的长为（ ）
| A、3cm | ||
| B、6cm | ||
C、
| ||
| D、9cm |
分析：先根据垂径定理求出OA、AM的长，再利用勾股定理求OM．
解答：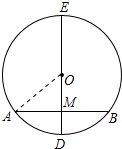
解：由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，
如图所示．直径ED⊥AB于点M，
则ED=10cm，AB=8cm，
由垂径定理知：点M为AB中点，
∴AM=4cm，
∵半径OA=5cm，
∴OM2=OA2-AM2=25-16=9，
∴OM=3cm．
故选：A．
解：由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，如图所示．直径ED⊥AB于点M，
则ED=10cm，AB=8cm，
由垂径定理知：点M为AB中点，
∴AM=4cm，
∵半径OA=5cm，
∴OM2=OA2-AM2=25-16=9，
∴OM=3cm．
故选：A．
点评：本题利用了垂径定理和勾股定理求解．
练习册系列答案
相关题目
过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm．则OM的长为（ ）
A、
| ||
B、
| ||
| C、2cm | ||
| D、3cm |
过⊙O内一点M的最长的弦长为4cm，最短的弦长为2cm，则OM的长为（ ）
A、
| ||
B、
| ||
| C、1cm | ||
| D、3cm |