题目内容
过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm，则OM的长为分析：圆内最长的弦为直径，最短的弦是过点M且与这条直径垂直的弦，由勾股定理和垂径定理求解即可．
解答：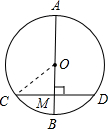
解：如图，∵AB=6cm，CD=4cm，
∴由垂径定理OC=3cm，CM=2cm，
∴由勾股定理得OM=
=
=
cm，
故答案为
．
解：如图，∵AB=6cm，CD=4cm，∴由垂径定理OC=3cm，CM=2cm，
∴由勾股定理得OM=
| OC2-CM2 |
| 32-22 |
| 5 |
故答案为
| 5 |
点评：本题综合考查了垂径定理和勾股定理．解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
练习册系列答案
相关题目
过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm．则OM的长为（ ）
A、
| ||
B、
| ||
| C、2cm | ||
| D、3cm |
过⊙O内一点M的最长弦长为10cm，最短弦长为8cm，那么OM的长为（ ）
| A、3cm | ||
| B、6cm | ||
C、
| ||
| D、9cm |
过⊙O内一点M的最长的弦长为4cm，最短的弦长为2cm，则OM的长为（ ）
A、
| ||
B、
| ||
| C、1cm | ||
| D、3cm |