题目内容
已知二次函数y=x2-4x+a，下列说法：①当x＜2时，y随x的增大而减小；
②若图象与x轴有交点，则a≤4；
③当a=3时，不等式x2-4x+a＞0的解集是1＜x＜3；
④若将图象向上平移1个单位，再向左平移3个单位后过点（1，-2），则a=-3．
其中正确的有
分析：根据函数解析式，画出草图．
①此函数在对称轴的左边是随着x的增大而减小，在右边是随x增大而增大，据此作答；
②和x轴有交点，就说明△≥0，易求a的取值；
③解一元二次不等式即可；
④根据左加右减，上加下减作答即可．
①此函数在对称轴的左边是随着x的增大而减小，在右边是随x增大而增大，据此作答；
②和x轴有交点，就说明△≥0，易求a的取值；
③解一元二次不等式即可；
④根据左加右减，上加下减作答即可．
解答：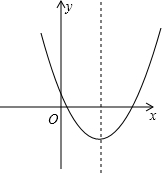
解：∵y=x2-4x+a，
∴对称轴x=2，
此二次函数的草图如图：
①当x＜1时，y随x的增大而减小，此说法正确；
②当△=b2-4ac=16-4a≥0，即a≥4时，二次函数和x轴有交点，此说法正确；
③当a=3时，不等式x2-4x+a＞0的解集是x＜1或x＞3，此说法错误；
④y=x2-4x+a配方后是y=（x-2）2+a-4，向上平移1个单位，再向左平移3个单位后，函数解析式是y=（x+1）2+a-3，把（1，-2）代入函数解析式，易求a=-3，此说法正确．
故答案为：①②④．
解：∵y=x2-4x+a，∴对称轴x=2，
此二次函数的草图如图：
①当x＜1时，y随x的增大而减小，此说法正确；
②当△=b2-4ac=16-4a≥0，即a≥4时，二次函数和x轴有交点，此说法正确；
③当a=3时，不等式x2-4x+a＞0的解集是x＜1或x＞3，此说法错误；
④y=x2-4x+a配方后是y=（x-2）2+a-4，向上平移1个单位，再向左平移3个单位后，函数解析式是y=（x+1）2+a-3，把（1，-2）代入函数解析式，易求a=-3，此说法正确．
故答案为：①②④．
点评：本题考查了二次函数的性质，解题的关键是掌握有关二次函数的增减性、与x轴交点的条件、与一元二次不等式的关系、上下左右平移的规律．
练习册系列答案
优学名师名题系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．