题目内容
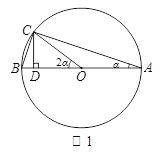
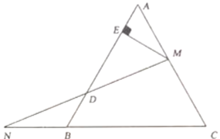
【题目】如图,![]() ,
,![]() ,且
,且![]() ,
,![]() ,点
,点![]() 以每秒
以每秒![]() 的速度从点
的速度从点![]() 开始沿射线
开始沿射线![]() 运动,同时点
运动,同时点![]() 在线段
在线段![]() 上由点
上由点![]() 向终点
向终点![]() 运动.设运动时间为
运动.设运动时间为![]() 秒.
秒.
(1)当![]() 时,
时,![]() ________
________![]() ,
,![]() __________
__________![]() .
.
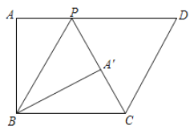
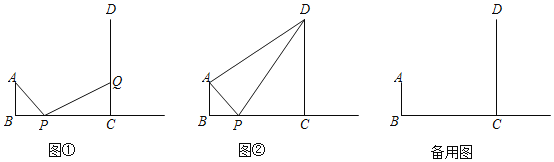
(2)如图①,当点![]() 与点
与点![]() 经过几秒时,使得
经过几秒时,使得![]() 与
与![]() 全等?此时,点
全等?此时,点![]() 的速度是多少?(写出求解过程)
的速度是多少?(写出求解过程)
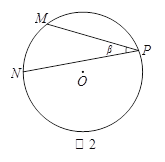
(3)如图②,是否存在点![]() ,使得
,使得![]() 是等腰三角形?若存在,请直接写出
是等腰三角形?若存在,请直接写出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)1,3;(2)若使得![]() 与
与![]() 全等,点
全等,点![]() 和点
和点![]() 经过6秒,此时点
经过6秒,此时点![]() 的速度为
的速度为![]() ;或点
;或点![]() 和点
和点![]() 经过4秒,此时点
经过4秒,此时点![]() 的速度为
的速度为![]() ;(3)存在,2或14或
;(3)存在,2或14或![]() 或
或![]()
【解析】
(1)根据路程与速度的关系解决问题即可;
(2)分两种情形:①△ABP≌AQCP;②△ABP≌△PCQ,分别构建方程解决问题即可;
(3)分三种情形:①AD=DP;②AD=AP;③PA=PD,分别构建方程即可解决问题.
(1)解:t=2时,![]() ,
,
∵BC=4cm,∴![]()
故答案为:1;3.
(2)若使![]() 与
与![]() 全等,需分两种情况:
全等,需分两种情况:
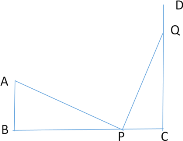
①当![]() 且
且![]() 时,如解图1,则△ABP≌△PCQ(SAS),
时,如解图1,则△ABP≌△PCQ(SAS),
![]()
∴![]()
解得![]() ,此时
,此时![]()
∴点![]() 的速度为
的速度为![]()
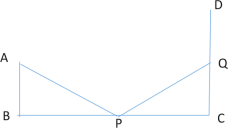
②当![]() 且
且![]() 时,△ABP≌QCP
时,△ABP≌QCP
![]()
即![]()
解得![]() ,此时
,此时![]()
∴点![]() 的速度为
的速度为![]()
综上所述,若使得![]() 与
与![]() 全等,点
全等,点![]() 和点
和点![]() 经过6秒,此时点
经过6秒,此时点![]() 的速度为
的速度为![]() ;或点
;或点![]() 和点
和点![]() 经过4秒,此时点
经过4秒,此时点![]() 的速度为
的速度为![]() ;
;
(3)2或14或![]() 或
或![]() ,理由是:
,理由是:
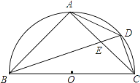
如图②中,作AH⊥CD于H,
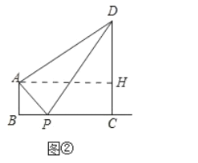
在Rt△ADH中,
AH=BC=4,DH=CD-CH=CD-AB=3,
∴AD=![]() ,
,
∵PA=![]()
DP=![]()
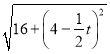
①当AD=PD时,
即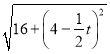 =5
=5
解得:t=2或者14
②当AD=AP时,
![]() =5
=5
解得t=![]() 或
或![]() (
(![]() 不符合题意舍弃)
不符合题意舍弃)
∴t=![]()
③当PA=PD时, ![]() =
=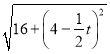
解得t=![]()
综上所述,满足条件的t的值为2或14或![]() 或
或![]()

练习册系列答案
相关题目