题目内容
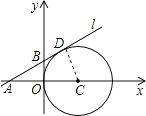
【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(2,0),直线l过点A(﹣2,0),与⊙C相切于点D,求直线l的解析式. 
【答案】解:如图所示,当直线l在x轴的上方时,
连接CD,
∵直线l为⊙C的切线,
∴CD⊥AD.
∵C点坐标为(2,0),
∴OC=2,即⊙C的半径为2,
∴CD=OC=2.
又∵点A的坐标为(﹣2,0),
∴AC=4,
∴AC=2CD,
∴∠CAD=30°,
在Rt△AOB中,OB=OAtan30°= ![]() ,
,
即B(0, ![]() ),
),
设直线l解析式为:y=kx+b(k≠0),则  ,
,
解得k= ![]() ,b=
,b= 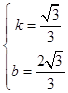 ,
,
∴直线l的函数解析式为y= ![]() x+
x+ ![]() .
.
同理可得,当直线l在x轴的下方时,直线l的函数解析式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
故直线l的函数解析式为y= ![]() x+
x+ ![]() 或y=﹣
或y=﹣ ![]() x﹣
x﹣ ![]() .
.
【解析】连接CD,由于直线l为⊙C的切线,故CD⊥AD.结合点与坐标的性质求得点B的坐标,设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
【考点精析】利用确定一次函数的表达式和切线的性质定理对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目






