Question

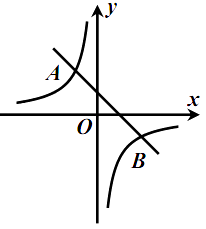
【题目】如图，已知 A (－4，n)， B (2，－4)是一次函数 y＝kx+b的图象和反比例函数的图象的两个交点．

（1）求反比例函数和一次函数的关系式；

（2）求直线 AB 与 x 轴的交点 C 的坐标及△ AOB 的面积；

（3）求方程 kx+b－＝0的解(请直接写出答案)；

（4）求不等式 kx+b－＜0的解集(请直接写出答案)．

Answer 1

【答案】（1）y=-，y=-x-2（2）6（3）x1＝-4，x2=2（4）－4＜x＜0或 x＞2

【解析】试题分析：（1）（1）先根据点B的坐标求出反比例函数的解析式为y=，再求出A的坐标是（-4， 2），利用待定系数法求一次函数的解析式即可；

（2）根据直线AB的解析式求出点C的坐标，求得OC的长，再根据S △ AOB ＝ S △ ACO + S △ BCO即可求得面积；

（3）方程kx+b-=0的解，就是求一次函数y=kx+b的图象和反比例函数y=的图象的交点的横坐标；

（4）求不等式kx+b-＜0的解集就是求一次函数y=kx+b的函数值小于反比例函数y=的函数值的自变量的取值范围.

试题解析：（1）因为 B (2，－4)在函数y=的图象上，所以 m ＝－8，

所以反比例函数的关系式为y=，

因为点 A (－4， n )在函数y=的图象上，所以 n ＝2，

因为 y ＝ kx + b 经过 A (－4，2)， B (2，－4)，

所以，解得，

所以一次函数的关系式为 y ＝－ x －2；

（2）因为 C 是直线 AB 与 x 轴的交点，

所以当 y ＝0时， x ＝－2，所以点 C (－2，0)，

所以 OC ＝2， S △ AOB ＝ S △ ACO + S △ BCO ＝×2×2+×2×4＝6；

（3）方程kx+b-=0的解，相当于一次函数y=kx+b的图象和反比例函数y=的图象的交点的横坐标，

即x1=-4，x2=2．

（4）不等式kx+b-＜0的解集相当于一次函数y=kx+b的函数值小于反比例函数y=的函数值，

从图象可以看出：-4＜x＜0或x＞2．