题目内容
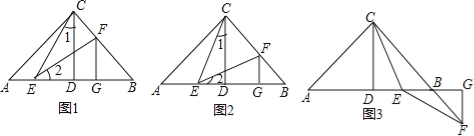
【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+![]() ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-![]() ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( )

A. 0个B. 1个C. 2个D. 3个
【答案】C
【解析】
根据三角形的内角和外角之间的关系计算.
解:(1)∵若P点是∠ABC和∠ACB的角平分线的交点,
∴∠ABP=∠PBC,∠ACP=∠PCB
∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)
∠P=180°-(∠PBC+∠PCB)
∴∠P=90°+![]() ∠A;
∠A;
故(1)的结论正确;
(2)∵∠A=∠ACB-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)
∠P=∠PCE-∠PBC
∴2∠P=∠A
故(2)的结论是错误.
(3)∠P=180°-(∠PBC+∠PCB)
=180°-![]() (∠FBC+∠ECB)
(∠FBC+∠ECB)
=180°-![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°-![]() (∠A+180°)
(∠A+180°)
=90°-![]() ∠A.
∠A.
故(3)的结论正确.
正确的为:(1)(3).
故选:C

练习册系列答案
相关题目