题目内容
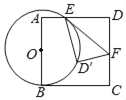
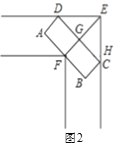
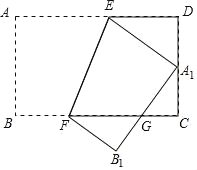
【题目】如图，将矩形ABCD沿EF对折，点A1恰好落在CD边上的中点处，线段A1B1交BC于点G，若AB＝6，AD＝9，则CG的长度为______.
【答案】
【解析】
由折叠的性质可得AE＝A1E，A1D＝3＝A1C，∠EA1G＝90°，由勾股定理可得DE＝4，通过证明△A1DE∽△CGA1，可得
，可求CG的长.
解：如图，
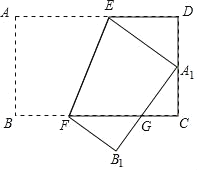
∵四边形ABCD是矩形，
∴AB＝CD＝6，∠D＝∠C＝90°
∵将矩形ABCD沿EF对折，点A1恰好落在CD边上的中点处，
∴AE＝A1E，A1D＝3＝A1C，∠EA1G＝90°，
∵A1E2＝DE2+A1D2，
∴(9﹣DE)2＝DE2+9，
∴DE＝4，
∵∠DEA1+∠DA1E＝90°，∠EA1D+∠GA1C＝90°，
∴∠DEA1＝∠GA1C，∠D＝∠C＝90°
∴△A1DE∽△CGA1，
∴
∴
，
∴GC＝.
故答案为：
练习册系列答案
相关题目
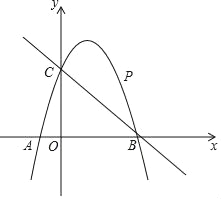
【题目】已知函数y＝y1y2，其中y1＝
+1，y2＝
x﹣1，请对该函数及其图象进行如下探究：
解析式探究：根据给定的条件，可以确定出该函数的解析式为：______.
函数图象探究：①根据解析式，完成下表：
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m＝______，n＝_____.
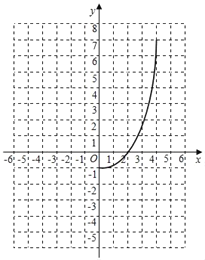
②根据表中数据，在如图所示的平面直角坐标系中描点，并画出当x≤0时的函数图象；
结合画出的函数图象，解决问题：
①若A(x1，y1)、B(x2，y2)为图象上的两点，满足x1＜x2；则y1_____y2(用＜、＝、＞填空).
②写出关于x的方程y1y2＝﹣x+3的近似解(精确到0.1).
