题目内容
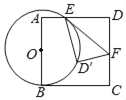
【题目】如图,在△ABC中,AB=AC,以AB为直径的QO分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
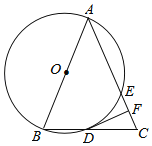
(1)求证:DF是⊙O的切线;
(2)求证:∠EDF=∠DAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接OD,求出OD⊥DF,根据切线的判定求出即可;
(2)连接BE,求出∠FDC=∠EBC,∠FDC=∠EDF,即可求出答案.
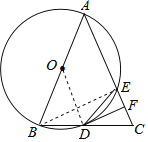
(1)证明:连接OD,
∵AB=AC,OB=OD,
∴∠ABC=∠C,∠ABC=∠ODB,
∴∠ODB=∠C,
∴AC∥OD,
∵DF⊥AC,
∴DF⊥OD,
∵OD过O,
∴DF是⊙O的切线;
(2)证明:连接BE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴BE∥DF,
∴∠FDC=∠EBC,
∵∠EBC=∠DAC,
∴∠FDC=∠DAC,
∵A、B、D、E四点共圆,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∵DF⊥AC,
∴∠EDF=∠FDC,
∴∠EDF=∠DAC.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目