题目内容
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.

(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.

(1)a=-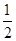 ,b=
,b=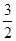 ;(2)-
;(2)-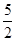 ≤y≤2;(3)点D’在该二次函数的图象上.
≤y≤2;(3)点D’在该二次函数的图象上.
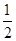 ,b=
,b=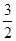 ;(2)-
;(2)-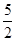 ≤y≤2;(3)点D’在该二次函数的图象上.
≤y≤2;(3)点D’在该二次函数的图象上.试题分析:(1)把C点坐标代入抛物线解析式,救出b的值;抛物线的对称轴是直线x=-1,顶点坐标是(-1,2),可求得a=-
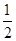 ;
;(2)根据-2≤x≤2,判断出二次函数y的取值范围;
(3)先求出点D的坐标,再确定它关于x轴对称的D’的坐标,再判定出它是否在该二次函数的图象上.
试题解析:(1)抛物线的对称轴是直线x=-1,顶点坐标是(-1,2)
可求得a=-
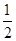 ,b=
,b=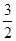
(2)当-2≤x≤2时,-
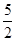 ≤y≤2
≤y≤2(3)点D坐标是(―2,―
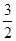 )
)点D’坐标是(―2,
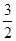 )
)经检验,点D’在该二次函数的图象上

练习册系列答案
相关题目
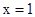 的抛物线的解析式 .
的抛物线的解析式 .


 的顶点坐标是 .
的顶点坐标是 .