题目内容
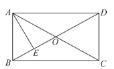
【题目】如图,在矩形ABCD中,AE⊥BD,垂足为点E,若BE=OE=1 cm,则∠AOB=______,S矩形ABCD=_______.
【答案】60° 4![]()
![]()
【解析】
根据矩形的性质可知,对角线相等且互相平分,可得AO=BO,由已知可得AE垂直平分BO,可证得△ABO是等边三角形,即得∠AOB=60°,利用勾股定理进而求出等边△ABO的面积,即可求出矩形ABCD的面积.
∵BE=OE=1cm,AE⊥BD,
∴OB=2cm, AE是BO的垂直平分线,
∴AB=AO,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∴AO=BO=AB=2cm,
∴△ABO是等边三角形,∠AOB=60°,
由勾股定理得:AE=![]() (cm),
(cm),
∴![]() (
(![]() ),
),
根据三角形等底等高面积相等,则矩形ABCD的面积=4![]() =4
=4![]() (
(![]() ),
),
故答案为:60°,4![]()
![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目