题目内容
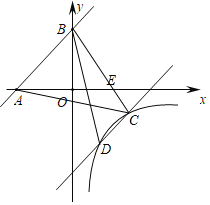
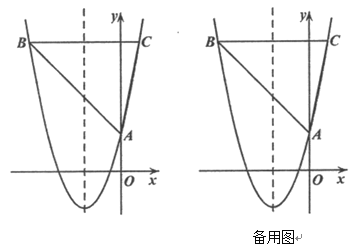
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:GD为⊙O切线;
(2)求证:DE2=EF·AC;
(3)若tan∠C=2,AB=5,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=3.
【解析】
(1)欲证明FG是⊙O的切线,只要证明OD⊥FG;
(2) 连接AD,然后求证Rt△CDF∽Rt△CAD,即可解答;
(3)由题意得出∠ABC=∠C,tan∠ABC=tan∠C=![]() ,根据直角三角形的三角函数得出CF=1,即可解答.
,根据直角三角形的三角函数得出CF=1,即可解答.
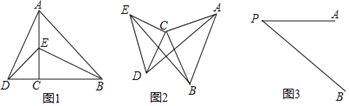
解:(1)如答图1,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵AB=AC,
∴∠ABC=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DG⊥AC,
∴OD⊥DF,
∴GD为⊙O切线;
(2)如答图2,连接AD,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴CD=BD,∠EAD=∠BAD,
∴BD=DE=CD,
∵DF⊥AC,
∴CF=EF,
∵Rt△CDF∽Rt△CAD,
∴![]() ,即CD2=CF·AC,
,即CD2=CF·AC,
∴DE2=EF·AC;
(3)如答图2,∵AB=AC,
∴∠ABC=∠C,tan∠ABC=tan∠C=![]() ,∵AB=5,
,∵AB=5,
∴BD=DC=![]() ,在Rt△CDF中,
,在Rt△CDF中,
∵tan∠C=2,∴CF=1,由(2)知,,EF=CF,
∴EF=CF=1,CE=2,所以AE=AC-CE=AB-CE=5-2=3.
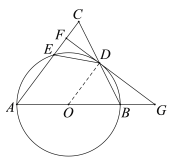
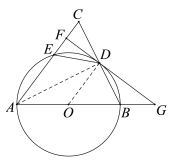
答图1 答图2

【题目】某果园有![]() 棵橘子树,平均每一棵树结
棵橘子树,平均每一棵树结![]() 个橘子.根据经验估计,每多种
个橘子.根据经验估计,每多种![]() 棵树,平均每棵树就会少结
棵树,平均每棵树就会少结![]() 个橘子.设果园增种
个橘子.设果园增种![]() 棵橘子树,果园橘子总个数为
棵橘子树,果园橘子总个数为![]() 个.
个.
(1)根据题意,填写下表:
增种的橘子树(棵) |
|
|
|
| … |
|
平均每棵树结橘子数(个) |
|
(2)求果园里增种多少棵橘子树时,所结橘子总数最多,并求出此时橘子的总数.