题目内容
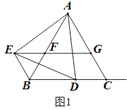
【题目】如图①,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 四点,动点
四点,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动(
运动(![]() 不与点
不与点![]() 、点
、点![]() 重合),设运动时间为
重合),设运动时间为![]() (秒).
(秒).
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 在(
在(![]() )中的抛物线上,当
)中的抛物线上,当![]()
![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求点
,求点![]() 的坐标;
的坐标;
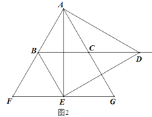
(3)当![]() 在
在![]() 上运动时,如图②.过点
上运动时,如图②.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(4)点![]() 为
为![]() 轴上一点,直线
轴上一点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,直接写出符合条件的所有
为等腰三角形?若存在,直接写出符合条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
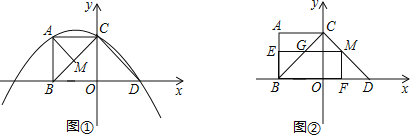
【答案】(1)![]() (2)
(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)设函数解析式为y=ax2+bx+c,将点A(﹣2,2),C(0,2),D(2,0)代入解析式即可;
(2)由已知易得点P为AB的垂直平分线与抛物线的交点,点P的纵坐标是1,则有1=![]() ,即可求P;
,即可求P;
(3)设点Q(m,0),直线BC的解析式y=﹣x+2,直线AQ的解析式![]() ,求出点
,求出点![]() ,
,![]() ,由勾股定理可得
,由勾股定理可得 ,
, ,
, ,分三种情况讨论△HOK为等腰三角形即可;
,分三种情况讨论△HOK为等腰三角形即可;
解:(1)设函数解析式为![]() c,
c,
将点![]() 代入解析式可得
代入解析式可得
 ,
,
 ,
,
![]() ;
;
(2)![]() ,
,
![]() ,
,
![]() 点
点![]() 为
为![]() 的垂直平分线与抛物线的交点,
的垂直平分线与抛物线的交点,
![]() ,
,
∴点![]() 的纵坐标是
的纵坐标是![]() ,
,
![]()
![]() ,
,
![]() 或
或![]() ,
,
∴![]() 或
或![]() ;
;
(3)![]() ,
,
![]() t,
t,
![]() ,
,
![]() ,
,
 ;
;
当![]() 时,
时,![]() 最大值为
最大值为![]() ;
;
(3)设点![]() ,直线
,直线![]() 的解析式
的解析式![]() ,
,
直线![]() 的解析式
的解析式![]() ,
,
∴![]() ,
,![]() ,
,
∴ ,
, ,
, ,
,
①![]() 时,
时,
 ,
,
![]() ,
,
![]() 或
或![]() ;
;
②![]() 时,
时,
 ,
,
![]() ,
,
![]() 或
或![]() ;
;
③![]() K时,
K时,
 ,不成立;
,不成立;
综上所述:![]() 或
或![]() 或
或![]() 或
或![]() ;
;

【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?