题目内容
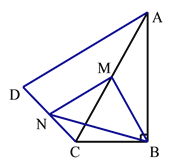
【题目】如图,在四边形ABCD中,∠ABC=90°![]() ,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分![]() ,AC=2, 写出求BN长的思路.
,AC=2, 写出求BN长的思路.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)分别根据“斜边上的中线等于斜边的一半”与中位线定理得到边之间的关系,再结合已知条件进行等量代换即可。(2))由已知可证∠DAC=∠CAB=30°,BM=AM=![]() AC=1,根据三角形外角性质可证∠CMB=60°,根据三角形中位线定理可证MN∥AD,MN=
AC=1,根据三角形外角性质可证∠CMB=60°,根据三角形中位线定理可证MN∥AD,MN=![]() AD=1, ∠DAC=∠NMC=30°可得三角形NMB是直角三角形,根据三角形勾股定理可得出BN的长
AD=1, ∠DAC=∠NMC=30°可得三角形NMB是直角三角形,根据三角形勾股定理可得出BN的长![]() .
.
试题解析:
(1)证明:∵∠ABC=90°,M为AC中点
∴BM=![]() AC
AC
∵M为AC中点,N为DC中点
∴MN=![]() AD
AD
∵AD=AC
∴BM=MN

(2)由已知可证∠DAC=∠CAB=30°,
BM=AM=![]() AC=1
AC=1
根据三角形外角性质可证∠CMB=60°
根据三角形中位线定理可证MN∥AD,MN=![]() AD=1, ∠DAC=∠NMC=30°
AD=1, ∠DAC=∠NMC=30°
可得三角形NMB是直角三角形
根据三角形勾股定理可得出BN的长![]()

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目