题目内容
【题目】如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ![]() ,则MN的长为。
,则MN的长为。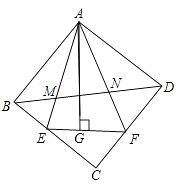
【答案】![]()
【解析】解:如图,连接GM,GN,
∵AG=AB,AE=AE,
∴△AGE≌△ABE,
同理可证△AGF≌△ADF,
∴BE=EG=4,DF=FG=6,
设正方形的边长为a,在Rt△CEF中,CE=a-4,CF=a-6,
由勾股定理,得CE2+CF2=EF2 , 即(a-4)2+(a-6)2=102 ,
解得a=12或-2(舍去负值),
∴BD=12 ![]() , 易证△ABM≌△AGM,△ADN≌△AGN,
, 易证△ABM≌△AGM,△ADN≌△AGN,
∴MG=BM=3 ![]() ,NG=ND=1
,NG=ND=1 ![]() -3
-3 ![]() -MN=9
-MN=9 ![]() -MN, ∠MGN=∠MGA+∠NGA=∠MBA+∠NDA=90°,
-MN, ∠MGN=∠MGA+∠NGA=∠MBA+∠NDA=90°,
在Rt△GMN中,由勾股定理,得MG2+NG2=MN2 , 即(3 ![]() )2+(9
)2+(9 ![]() -MN)2=MN2 ,
-MN)2=MN2 ,
解得MN=5 ![]()
所以答案是:5 ![]() .
.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
相关题目













