题目内容
【题目】八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分. ①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
【答案】
(1)解: ![]() =
= ![]() =82.5(分),
=82.5(分),
答:A,B,C,D四位同学成绩的平均分是82.5分
(2)解:①设E同学答对x题,答错y题,由题意得
![]() ,
,
解得 ![]() ,
,
答:E同学答对12题,答错1题.
②C同学,他实际答对14题,答错3题,未答3题
【解析】(1)直接算出A,B,C,D四位同学成绩的总成绩,再进一步求得平均数即可;(2)①设E同学答对x题,答错y题,根据对错共20﹣7=13和总共得分58列出方程组成方程组即可;②根据表格分别算出每一个人的总成绩,与实际成绩对比:A为19×5=95分正确,B为17×5+2×(﹣2)=81分正确,C为15×5+2×(﹣2)=71错误,D为17×5+1×(﹣2)=83正确,E正确;所以错误的是C,多算7分,也就是答对的少一题,打错的多一题,由此得出答案即可.

【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定: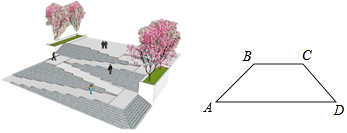
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.