题目内容
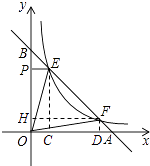
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
【答案】2;![]()
【解析】解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,
∵△OEP的面积为1,
∴ ![]() |k|=1,
|k|=1,
而k>0,
∴k=2,
∴反比例函数解析式为y= ![]() ,
,
∵EP⊥y轴,FH⊥y轴,
∴EP∥FH,
∴△BPE∽△BHF,
∴ ![]() =
= ![]() ,即HF=mPE,
,即HF=mPE,
设E点坐标为(t, ![]() ),则F点的坐标为(tm,
),则F点的坐标为(tm, ![]() ),
),
∵S△OEF+S△OFD=S△OEC+S梯形ECDF ,
而S△OFD=S△OEC=1,
∴S△OEF=S梯形ECDF= ![]() (
( ![]() +
+ ![]() )(tm﹣t)
)(tm﹣t)
=( ![]() +1)(m﹣1)
+1)(m﹣1)
= ![]() .
.
所以答案是:2, ![]() .
.
【考点精析】掌握反比例函数的性质是解答本题的根本,需要知道性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

练习册系列答案
相关题目

