Question

【题目】一条笔直的公路上有甲、乙两地相距2400米，王明步行从甲地到乙地，每分钟走96米，李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发，运动的时间为（分），与乙地的距离为（米），图中线段EF，折线分别表示两人与乙地距离和运动时间之间的函数关系图象

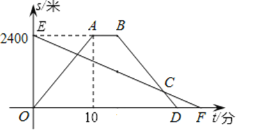
（1）李越骑车的速度为 米/分钟；F点的坐标为 ；

（2）求李越从乙地骑往甲地时， 与之间的函数表达式；

（3）求王明从甲地到乙地时， 与之间的函数表达式；

（4）求李越与王明第二次相遇时的值．

Answer 1

【答案】（1）240；（25，0）；（2）s＝240t；（3）s＝﹣96x+2400；（4）20

【解析】

（1）由函数图象中的数据可以计算出李越骑车的速度，根据王明步行的速度可得F点的坐标；

（2）运用待定系数法，即可求出李越从乙地骑往甲地时，s与t之间的函数表达式；

（3）运用待定系数法，可得王明从甲地到乙地时，s与t之间的函数表达式；

（4）根据第二次相遇时李越走的路程-王明走的路程=2400米列方程解答即可．

（1）解：由图象可得，

李越骑车的速度为：2400÷10=240米/分钟，2400÷96=25，所以F点的坐标为（25，0）．

故答案为： 240；(25，0)；

（2）设李越从乙地骑往甲地时，s与t之间的函数表达式为s＝kt，

把(10，2400)代入得，

2400＝10k，得k＝240，

即李越从乙地骑往甲地时，s与t之间的函数表达式为s＝240t

（3）设王明从甲地到乙地时，s与t之间的函数表达式为s＝kt+2400，把(25，0)代入得，

25k+2400＝0，解得k＝﹣96， 所以王明从甲地到乙地时，s与t之间的函数表达式为：s＝﹣96x+2400；

（4）根据题意得，240（t﹣2）﹣96t＝2400，解得t＝20．