题目内容
如图,第①个图形中一共有1个平行四边形,第②个图形中有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑨个图形中平行四边形的个数是( )


| A、54 | B、110 | C、89 | D、109 |
考点:规律型:图形的变化类
专题:
分析:每一个图形分两部分查出平行四边形的个数,然后写出第n个图形的平行四边形的个数的表达式,在把n=9代入进行计算即可得解.
解答:解:第1个图形有1个平行四边形,
第2个图形有5个平行四边形,5=2×
-1,
第3个图形有11个平行四边形,11=2×
-1,
第4个图形有19个平行四边形,19=2×
-1,
…,
第n个图形有2×
-1=n(n+1)-1个平行四边形,
当n=9时,9×(9+1)-1=89.
故选:C.
第2个图形有5个平行四边形,5=2×
| 2×3 |
| 2 |
第3个图形有11个平行四边形,11=2×
| 3×4 |
| 2 |
第4个图形有19个平行四边形,19=2×
| 4×5 |
| 2 |
…,
第n个图形有2×
| n(n+1) |
| 2 |
当n=9时,9×(9+1)-1=89.
故选:C.
点评:此题考查图形变化规律,查找平行四边形时要注意复合平行四边形,分两部分查找并写出第n个图形的平行四边形的个数是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知x2-2x-3=0,则2x2-4x的值为( )
| A、-6 | B、6 | C、-2或6 | D、-2或30 |
观察下列数表:
1 2 3 4…第一行
2 3 4 5…第二行
3 4 5 6…第三行
4 5 6 7…第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为( )
1 2 3 4…第一行
2 3 4 5…第二行
3 4 5 6…第三行
4 5 6 7…第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为( )
| A、2n-1 | B、2n+1 | C、n2-1 | D、n2 |
下列图形都是由同样大小的正方形按一定规律组成的,其中,第1个图形中一共有1个正方形,第2个图形中共有5个正方形,第3个图形中共有14个正方形,…,按照此规律第5个图形中正方形的个数为( )


| A、30 | B、46 | C、55 | D、60 |
如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有( )
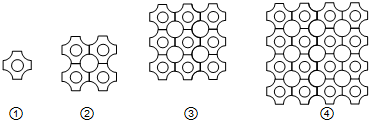

| A、100个 | B、101个 | C、181个 | D、221个 |
 如图,图①由3张同样大小的正方形纸片组成,图②由6张同样大小的小正方形纸片组成,图③由10张同样大小的小正方形纸片组成,…,以此规律组成第⑧图需要的同样大小的小正方形纸片张数为( )
如图,图①由3张同样大小的正方形纸片组成,图②由6张同样大小的小正方形纸片组成,图③由10张同样大小的小正方形纸片组成,…,以此规律组成第⑧图需要的同样大小的小正方形纸片张数为( )| A、28 | B、36 | C、45 | D、66 |
下列式子中( )是方程.
| A、2+3-X | B、3+X>5 | C、3-y=1 | D、以上都不是 |
方程|x|=-x的解是( )
| A、-1 | B、负整数 | C、所有负有理数 | D、所有非正有理数 |
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、居 | B、邯 | C、宜 | D、郸 |