题目内容
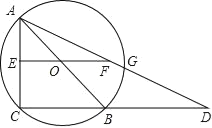
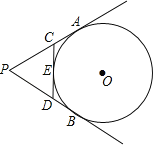
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
【答案】![]()
【解析】
试题连接OA、OB、OP,延长BO交PA的延长线于点F.利用切线求得CA=CE,DB=DE,PA=PB再得出PA=PB=![]() r.利用Rt△BFP∽Rt△OAF得出AF=
r.利用Rt△BFP∽Rt△OAF得出AF=![]() FB,在RT△FBP中,利用勾股定理求出BF,再求tan∠APB的值即可.
FB,在RT△FBP中,利用勾股定理求出BF,再求tan∠APB的值即可.
试题解析:连接OA、OB、OP,延长BO交PA的延长线于点F.
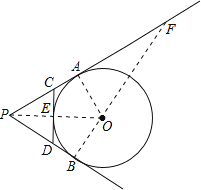
∵PA,PB切⊙O于A、B两点,CD切⊙O于点E
∴∠OAF=∠PBF=90°,CA=CE,DB=DE,PA=PB,
∵△PCD的周长=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=3r,
∴PA=PB=![]() r.
r.
在Rt△PBF和Rt△OAF中,
∠FAO=∠FBP
∠OFA=∠PFB,
∴Rt△PBF∽Rt△OAF.
∴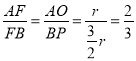
∴AF=![]() FB,
FB,
在Rt△FBP中,
∵PF2-PB2=FB2
∴(PA+AF)2-PB2=FB2
∴(![]() r+
r+![]() BF)2-(
BF)2-(![]() r)2=BF2,
r)2=BF2,
解得BF=![]() r,
r,
∴tan∠APB=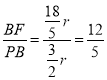 .
.

练习册系列答案
相关题目