题目内容
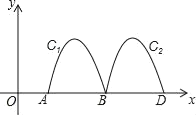
【题目】如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得到C2,C2与x轴交于B、D两点.若直线y=kx﹣k与C1、C2共有3个不同的交点,则k的最大值是( )
A.![]() B.2
B.2![]() ﹣6C.6+4
﹣6C.6+4![]() D.6﹣4
D.6﹣4![]()
【答案】C
【解析】
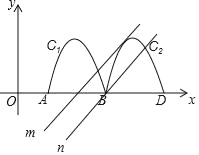
本题首先要确定直线可能所处的位置(如下图所示),一种情况是直线m与抛物线相切,另一种情况是直线n过B点,进而求出k的值.
解:
由抛物线从C1:y=﹣x2+4x﹣3平移得到抛物线C2,则容易得到其的方程为:
y=﹣(x﹣4)2+1,(3≤x≤5),
如图所示直线与图象有3个交点的情况如图所示,即在两条直线m、n之间部分作直线都会和抛物线图形有3个交点:
(1)当直线m与抛物线C2相切时,可得:kx﹣k=y=﹣(x﹣4)2+1
相切时:△=0,即k2﹣12k+4=0,解得:k=6±4![]() ,取最大值为6+4
,取最大值为6+4![]() ;
;
(2)当直线n过B点时,把B点坐标(3,0)代入直线y=kx﹣k,解得:k=0,
直线k>0;
综上,0<k≤6+4![]() ,
,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目