题目内容
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图),易证BM+DN=MN.
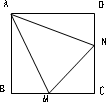
(1)当∠MAN绕点A旋转到BM≠DN时(如图),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
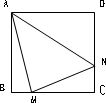
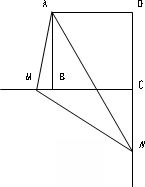
(2)当∠MAN绕点A旋转到如图的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
答案:
解析:
解析:
(1)BM+DN=MN成立.如图,把△ADN绕点A顺时针旋转90°,得到△ABE,则可证得E、B、M三点共线(图形画正确).

证得:∠EAM=∠NAM.证得:△AEM≌ANM.∴ME=MN.
∵ME=BE+BM=DN+BM∴DN+BM=MN.
(2)DN-BM=MN

练习册系列答案
相关题目
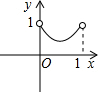
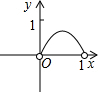
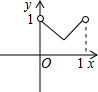
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )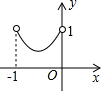
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=