题目内容
已知:正方形ABCD边长为4cm,E,F分别为CD,BC的中点,动点P在线段AB上从B?A以2cm/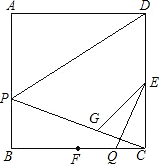 s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.(1)求证:△CQE∽△APD;
(2)问:在运动过程中CG•CP的值是否发生改变?如果不变,请求这个值;若改变,请说明理由;
(3)当t为何值时,△CGE为等腰三角形并求出此时△CGE的面积.
分析:(1)首先求出QC=2-t,AP=4-2t,求出线段比然后可证明△CQE∽△APD.
(2)依题意证得△CQE∽△APD后推出∠EGC=∠PDC,然后再证明△CGE∽△CDP利用线段比可证得CG•CP=CD•CE.
(3)由(2)得△CGE∽△CDP,要分三种情况讨论t的取值然后才能求出△CGE的面积.
(2)依题意证得△CQE∽△APD后推出∠EGC=∠PDC,然后再证明△CGE∽△CDP利用线段比可证得CG•CP=CD•CE.
(3)由(2)得△CGE∽△CDP,要分三种情况讨论t的取值然后才能求出△CGE的面积.
解答:(1)证明:∵FQ=t,BP=2t,
∴QC=2-t,AP=4-2t,
∴
=
=
,
∵∠QCE=∠A=90°,
∴△CQE∽△APD.(2分)
(2)解:CG•CP的值是一个定值.(3分)
∵△CQE∽△APD,
∴∠CQE=∠APD,
∵正方形ABCD中AB∥CD,
∴∠APD=∠PDC,
∵∠EGC=∠EQC,
∴∠EGC=∠PDC,
∵∠PCD=∠PCD,
∴△CGE∽△CDP,
∴
=
,
∴CG•CP=CD•CE=4×2=8.(5分)
(3)解:∵△CGE∽△CDP,
∴△CGE和△CDP的形状相同.
①t=0时△CDP为等腰三角形,则△CGE也为等腰三角形.(6分)
S△CGE=2.(7分)
②t=1时△CDP为等腰三角形,则△CGE也为等腰三角形.(8分)
∵
=(
)2,
∴
=(
)2,
S△CGE=
.(9分)
③t=2的时候∠EGC不存在.(10分)
综上所述t=0时,△CGE为了等腰三角形面积为2,
t=1时,△CGE为等腰三角形面积为
.(11分)
∴QC=2-t,AP=4-2t,
∴
| QC |
| AP |
| CE |
| AD |
| 1 |
| 2 |
∵∠QCE=∠A=90°,
∴△CQE∽△APD.(2分)
(2)解:CG•CP的值是一个定值.(3分)
∵△CQE∽△APD,
∴∠CQE=∠APD,
∵正方形ABCD中AB∥CD,
∴∠APD=∠PDC,
∵∠EGC=∠EQC,
∴∠EGC=∠PDC,
∵∠PCD=∠PCD,
∴△CGE∽△CDP,
∴
| CG |
| CD |
| CE |
| CP |
∴CG•CP=CD•CE=4×2=8.(5分)
(3)解:∵△CGE∽△CDP,
∴△CGE和△CDP的形状相同.
①t=0时△CDP为等腰三角形,则△CGE也为等腰三角形.(6分)
S△CGE=2.(7分)
②t=1时△CDP为等腰三角形,则△CGE也为等腰三角形.(8分)
∵
| S△CGE |
| S△CDP |
| CE |
| CP |
∴
| S△CGE |
| 8 |
| 2 | ||
2
|
S△CGE=
| 8 |
| 5 |
③t=2的时候∠EGC不存在.(10分)
综上所述t=0时,△CGE为了等腰三角形面积为2,
t=1时,△CGE为等腰三角形面积为
| 8 |
| 5 |
点评:本题考查了正方形的性质,相似三角形的判定,线段的比等知识,难度中上.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
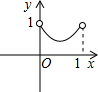
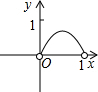
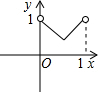
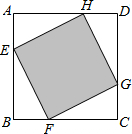 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )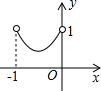
 由.
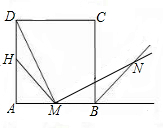
由. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.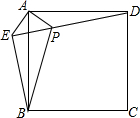 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=