��Ŀ����
С���糿�Ӽ���������ٲ���ȥ��ѧ��С����������С��������10���ӣ�����С������ѧ�α�û�������������Ͽα����������ﳵ��С����ѧ��·����С���������С��ͬʱ����ѧУ����֪С����������ѧ;�У������������ʱ�������ڵ�λ����ҵľ���Ϊ ǧ�ף���
ǧ�ף��� ��֮��ĺ�����ϵ��ͼ����ͼ�е����߶�
��֮��ĺ�����ϵ��ͼ����ͼ�е����߶� ��ʾ��
��ʾ��
��1���������߶� ����Ӧ�ĺ�����ϵʽ��
����Ӧ�ĺ�����ϵʽ��
��2�������ͼ���߶� ��ʵ�����壻
��ʵ�����壻
��3������������ͼ�л���С������������С���Ĺ����У�������λ����ҵľ��� ��ǧ�ף���С���������ʱ�䣨���ӣ�֮�亯����ϵ��ͼ���������ѣ���Ի�����ͼ�����������ʵ��ı�ע��
��ǧ�ף���С���������ʱ�䣨���ӣ�֮�亯����ϵ��ͼ���������ѣ���Ի�����ͼ�����������ʵ��ı�ע��
��1���߶�OA��Ӧ�ĺ�����ϵʽΪ��s= t��0��t��12��
t��0��t��12��
�߶�AB��Ӧ�ĺ�����ϵʽΪ��s=1��12��t��20����
��2��ͼ���߶�AB��ʵ�������ǣ�С������12���Ӻ�����������ΪԲ�ģ�1ǧ��Ϊ�뾶��Բ���ε�·�����ٲ�����8���ӣ�
��3��ͼ�μ�������
���������������1��OAΪ����������ͼ�����ô���ϵ���������
��2��AB����Ҿ���û�����仯˵�����Լ�ΪԲ���������˶���
��3��������ٶ�������С����2����������������·�ã�20��12����2=4���ӣ�
�����������1���߶�OA��Ӧ�ĺ�����ϵʽΪ��s= t��0��t��12��
t��0��t��12��
�߶�AB��Ӧ�ĺ�����ϵʽΪ��s=1��12��t��20����
��2��ͼ���߶�AB��ʵ�������ǣ�
С������12���Ӻ�����������ΪԲ�ģ�1ǧ��Ϊ�뾶��Բ���ε�·�����ٲ�����8���ӣ�
��3����ͼ���֪��С����20���ӵ���ѧУ����С�������軨20��10=10���ӵ���ѧУ����֪С��������ٶ���С����2��������С����12������1ǧ�ף������軨6������1ǧ�ף���D��16��1����С����20��12=8������Բ���ε�·�������軨4������Բ���ε�·����B��20��1����
�����ͼ����10��0����16��1����20��1����ͼ�����߶�CD��DB��������ͼ�� ��
��
���㣺һ�κ�����Ӧ�ã�

�±��У�y��x��һ�κ�����
| x |  2 2 | 1 | 2 | | 5 |
| y | 6 |  3 3 | |  12 12 |  15 15 |
��1����ú����ı���ʽ������ȫ����
��2����֪�ú���ͼ����һ��M��1��-3��Ҳ�ڷ���������
 ͼ���ϣ�������������ͼ�����һ����N�����꣮
ͼ���ϣ�������������ͼ�����һ����N�����꣮  ��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
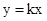 ���ᾭ��һ���̶��ĵ�
���ᾭ��һ���̶��ĵ� �����Ǿͳ�ֱ��
�����Ǿͳ�ֱ�� ȡ�κ�ʵ����������
ȡ�κ�ʵ���������� �������
������� ��ֱ��д������A�����ꣻ
��ֱ��д������A�����ꣻ ���ҡ�B����C�Ľ�ƽ���߷ֱ���y���ֱ��
���ҡ�B����C�Ľ�ƽ���߷ֱ���y���ֱ�� �����BC����ֱ�ߵı���ʽ��
�����BC����ֱ�ߵı���ʽ��
 ��ͼ���һ������ΪA(2, m)��
��ͼ���һ������ΪA(2, m)�� ��
�� ����һ�κ���
����һ�κ��� ��
�� ���ཻ��A��B���㣬AC��
���ཻ��A��B���㣬AC�� ���ڵ�C������OAC�����Ϊ1����tan��AOC=2��
���ڵ�C������OAC�����Ϊ1����tan��AOC=2�� ��ֵ����һ�κ���
��ֵ����һ�κ���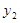 ��ֵ��
��ֵ��

