题目内容
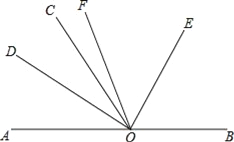
【题目】如图，点O为直线AB上一点，过点O作直线OC，已知∠AOC≠90°，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．求：
（1）当0°＜∠AOC＜90°时，求∠FOB+∠DOC的度数；
（2）若∠DOC=3∠COF，求∠AOC的度数．
【答案】（1）135°（2）∠AOC=67.5°或135°
【解析】（1）先根据射线OD平分∠AOC，∠AOD=∠COD，射线OE平分∠BOC，得∠COE=∠BOE，再根据∠AOC+∠BOC=180°，得出∠DOE=90°，由射线OF平分∠DOE，得∠DOF=∠EOF=45°，从而求得∠FOB+∠DOC的度数；
（2）设∠AOD=∠COD=x°，分∠AOC为锐角和钝角两种情况，根据∠DOC=3∠COF，得出x的值，即可求得∠AOC的度数．
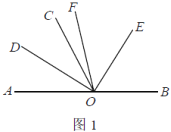
解：如图1，
（1）∵射线OD平分∠AOC，
∴∠AOD=∠COD，
∵射线OE平分∠BOC，
∴∠COE=∠BOE，
∵∠AOC+∠BOC=180°，
∴∠DOE=∠DOC+∠EOC=
∠AOC+∠BOC=90°，
∵OF平分∠DOE，
∴∠DOF=∠EOF=∠DOE=45°，
∴∠FOB+∠DOC=∠BOF+∠AOD=180°-∠DOF=280°-45°=135°；
（2）设∠AOD=∠COD=x°，则∠AOC=2x°，
由（1）的证明过程可知∠DOE=90°，∠DOF=∠EOF=45°，
∠AOC≠90°，分情况考虑如下：
①当∠AOC为锐角时，如图1，∠COF=∠DOF-∠COD=45°-x，
∵∠DOC=3∠COF，
∴x=3（45°-x），
解得x=33.75°，
∴∠AOC=2x=67.5°．
②当∠AOC为钝角时，如图2，
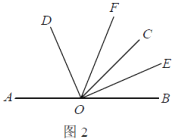
∠COF=∠COD-∠DOF=x-45°，
∵∠DOC=3∠COF，
∴x=3（x-45°），
解得x=67.5°，
∴∠AOC=2x=135°．
综合，可得∠AOC=67.5°或135°．
“点睛”本题考查了角的计算和角平分线的定义，一定要注意角平分线的几种表示方法．如：∠1=∠2，∠1=∠AOB，∠AOB=2∠1．
