Question

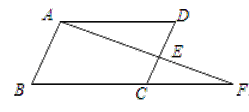
【题目】如图，点A，D是函数y= （k＞0，x＞0）图象上两点（点A在点D的左侧），直线AD分别交x，y轴于点E，F．AB⊥x轴于点B，CD⊥x轴于点C，连结AO，BD．若BC=OB+CE，S△AOF+S△CDE=1，则S△ABD= ．

Answer 1

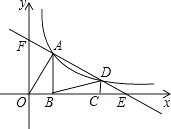
【答案】
【解析】解：设A（a， ），D（d， ），则d＞a，B（a，0），C（d，0）， ∵BC=d﹣a，BC=OB+CE，
∴OE=2BC=2d﹣2a，
∴E（2d﹣2a，0）．
∵tan∠AEB= = = ，
∴ = = ，
整理得3a2﹣4ad+d2=0，
（a﹣d）（3a﹣d）=0，
∵a﹣d≠0，
∴3a﹣d=0，
∴d=3a．
∵ = ，
∴OF= ．
∵S△AOF+S△CDE=1，
∴ × ×a+ ×（2d﹣2a﹣d）× =1，
∴k= ，
∴S△ABD=S梯形ABCD﹣S△BCD
= （ + ）（d﹣a）﹣ × ×（d﹣a）
= × ×（d﹣a）
= × ×（3a﹣a）
= ．
所以答案是 ．
【考点精析】认真审题，首先需要了解比例系数k的几何意义(几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积)．