题目内容
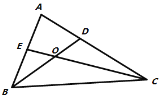
【题目】如图,已知:在![]() 中,
中,![]() ,
,![]() .
.

(1)作![]() 的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,判定直线AB与DE的位置关系,并对结论给予证明.
【答案】(1)见解析;(2)AB垂直平分DE.理由见解析
【解析】
(1)利用基本作图(作已知角的平分线)作BD平分∠ABC;作AB的垂直平分线即可得到AB的中点E;
(2)根据“SSS”可判断△ADE≌△BDE,然后再证明△BDC≌△BDE,得到∠BED=90°,即可解答.
(1)如图,BD为所作,如图,点E为所作;
(2)AB垂直平分DE.理由如下:
∵BD为角平分线,
∴∠ABD=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∵∠ABD=∠A=30°,
∴DB=DA,
在△ADE和△BDE中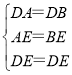 ,
,
∴△ADE≌△BDE.
∴∠AED=∠EDB,
∵∠CBD=30°,
∴∠BDC=60°,
∴∠AED=∠EDB=60°,
在△BDC和△BDE中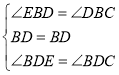
∴△BDC≌△BDE(ASA)
∴∠BED=90°,BE=AE,
∴AB垂直平分DE.

练习册系列答案
相关题目