题目内容
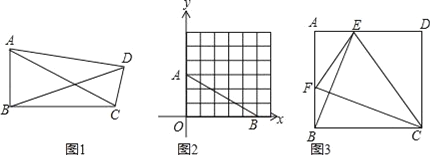
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位的速度沿
点以每秒2个单位的速度沿![]() 轴向左移动.
轴向左移动.
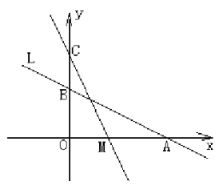
(1)求![]() 、
、![]() 两点的坐标
两点的坐标
(2)求![]() 的面积
的面积![]() 与
与![]() 的移动时间
的移动时间![]() (秒)之间的函数关系式;
(秒)之间的函数关系式;
(3)当![]() 何值时
何值时![]() ,并求此时
,并求此时![]() 点的坐标.
点的坐标.
(4)当![]() 何值时
何值时![]() 的面积是
的面积是![]() 一半,并求此时
一半,并求此时![]() 点的坐标.
点的坐标.
【答案】(1)A(9,0);(2)B(0,3);(2)S= ;(3)当t=3,M(3,0),当t=6,M(-3,0);(4)当t=
;(3)当t=3,M(3,0),当t=6,M(-3,0);(4)当t=![]() ,M(
,M(![]() ,0);当t=
,0);当t=![]() ,M(-
,M(-![]() ,0)
,0)
【解析】
(1)对于![]() ,令x=0可求出B点坐标,令y=0可求出A点坐标;
,令x=0可求出B点坐标,令y=0可求出A点坐标;
(2)分点M在原点左侧和右侧两种情况,根据三角形的面积公式解答即可;
(3)分点M在原点左侧和右侧两种情况,根据全等三角形的性质列式求出t的值,进而可求出点M的坐标;
(4)根据三角形的面积公式列式求出OM的长,进而分点M在原点左侧和右侧两种情况,可求出t的值及点M的坐标.
解:(1)当x=0时,y=3,
∴B(0,3).
当y=0时,![]() ,x=9,
,x=9,
∴A(9,0);
(2)9÷2=4.5秒,
当点M在原点右侧时,即0≤t≤4.5时,由题意得,OM=9-2t,
∴S=![]() =
=![]() .
.
当点M在原点左侧时,即t>4.5时,由题意得,OM=2t-9,
∴S=![]() =
=![]() ,
,
∴S= ;
;
(3)当点M在原点右侧时,即0≤t≤4.5时,
∵![]() ,
,
∴OM=OB,
∴9-2t=3,
∴t=3,
∴OM=9-6=3,
∴M(3,0);
当点M在原点左侧时,即t>4.5时,
∵![]() ,
,
∴OM=OB,
∴2t-9=3,
∴t=6,
∴OM=12-9=3,
∴M(-3,0);
综上可知,当t=3,M(3,0),当t=6,M(-3,0);
(4)S△AOB=![]() ,
,
∵S△COM=![]() S△AOB,
S△AOB,
∴![]() ,
,
∴OM=![]() ,
,
当点M在原点右侧时,
9-2t=![]() ,
,
∴t=![]() ,
,
此时M(![]() ,0);
,0);
当点M在原点左侧时,
2t-9=![]() ,
,
∴t=![]() ,
,
此时M(-![]() ,0),
,0),
综上可知,当t=![]() ,M(
,M(![]() ,0);当t=
,0);当t=![]() ,M(-
,M(-![]() ,0).
,0).