题目内容
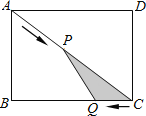
【题目】如图，已知
为
的直径，
是的切线，连接
交于点
取
的中点
，连接
交于点
，过点作
于点
．
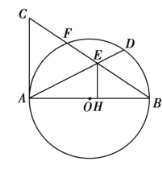
（1）求证：
；
（2）若
，
，求和
的长．
【答案】（1）见解析；（2）
，
【解析】
（1）利用切线的性质得AB⊥AC，则可判断EH∥AC，然后根据相似三角形的判定方法得到结论；
（2）连接AF，如图，利用圆周角定理得到∠AFB=90°，则可判定△CAF∽△CBA，利用相似比可计算出CA=12，再利用D点为弧BF的中点得到∠BAD=∠FAD，根据角平分线的性质定理得到EF=EH，设EH=x，则EF=x，BE=10-x，由于△HBE∽△ABC，则利用相似比求出x即可．
（1）
为
的直径，
是的切线，
，又
，
，
．
（2）连接
，
为的直径，
，
，
又
，
，
，
，
．
为
的中点，
，
又
，，
．
设
，则
，
，
由（1）知
，
，
，
，即．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校拟派一名跳高运动员参加校际比赛，对甲、乙两名同学进行了8次跳高选拔比赛，他们的原始成绩（单位：cm）如下表：
学生/成绩/次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
甲 | 169 | 165 | 168 | 169 | 172 | 173 | 169 | 167 |
乙 | 161 | 174 | 172 | 162 | 163 | 172 | 172 | 176 |
两名同学的8次跳高成绩数据分析如下表：
学生/成绩/名称 | 平均数（单位：cm） | 中位数（单位：cm） | 众数（单位：cm） | 方差（单位：cm2） |
甲 | a | b | c | 5.75 |
乙 | 169 | 172 | 172 | 31.25 |
根据图表信息回答下列问题：
（1）a＝ ，b＝ ，c＝ ；
（2）这两名同学中， 的成绩更为稳定；（填甲或乙）
（3）若预测跳高165就可能获得冠军，该校为了获取跳高比赛冠军，你认为应该选择 同学参赛，理由是： ；
（4）若预测跳高170方可夺得冠军，该校为了获取跳高比赛冠军，你认为应该选择 同学参赛，班由是： ．
