题目内容
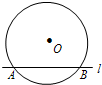
如图,在矩形ABCD的对角线AC上有一动点O,以OA为半径作⊙O交AD、AC于点E、F,连结CE.
(1)若CE恰为⊙O的切线,求证:∠ACB=∠DCE;
(2)在(1)的条件下,若AB=
,BC=2,求⊙O的半径.

(1)若CE恰为⊙O的切线,求证:∠ACB=∠DCE;
(2)在(1)的条件下,若AB=
| 2 |

(1)证明:连接OE,
∵CE是⊙O的切线,
∴OE⊥EC,
∴∠DEC+∠AEO=90°,
∵OE=OA,
∴∠AEO=∠EAO,
∵四边形ABCD是矩形,
∴AD∥BC,∠D=90°,
∴∠ACB=∠EAO,∠DCE+∠DEC=90°,
∴∠ACB=∠DCE;
(2)连接EF,
∵∠ACB=∠DCE,∠B=∠D=90°,
∴△ABC∽△EDC,
∴
=
,
∵AB=CD=
,BC=2,
∴DE=1,
∴AE=DE,
∵AF为直径,
∴EF⊥AD,
∴EF∥CD,
∴AF=CF,
在Rt△ABC中,AB=
,BC=2,
∴AC=
,
∴⊙O的半径OA=
AF=
AC=
.

∵CE是⊙O的切线,
∴OE⊥EC,
∴∠DEC+∠AEO=90°,
∵OE=OA,
∴∠AEO=∠EAO,
∵四边形ABCD是矩形,
∴AD∥BC,∠D=90°,
∴∠ACB=∠EAO,∠DCE+∠DEC=90°,
∴∠ACB=∠DCE;
(2)连接EF,
∵∠ACB=∠DCE,∠B=∠D=90°,
∴△ABC∽△EDC,
∴
| AB |
| DE |
| BC |
| CD |
∵AB=CD=
| 2 |
∴DE=1,
∴AE=DE,
∵AF为直径,
∴EF⊥AD,
∴EF∥CD,
∴AF=CF,
在Rt△ABC中,AB=
| 2 |
∴AC=
| 6 |
∴⊙O的半径OA=
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 4 |


练习册系列答案
相关题目

 ,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.
,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.