题目内容
已知抛物线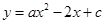 与它的对称轴相交于点
与它的对称轴相交于点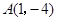 ,与
,与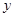 轴交于
轴交于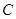 ,与
,与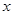 轴正半轴交于
轴正半轴交于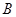 .
.
(1)求这条抛物线的函数关系式;
(2)设直线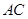 交
交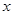 轴于
轴于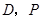 是线段
是线段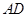 上一动点(
上一动点(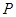 点异于
点异于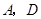 ),过
),过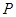 作
作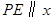 轴交直线
轴交直线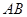 于
于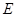 ,过
,过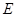 作
作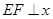 轴于
轴于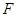 ,求当四边形
,求当四边形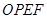 的面积等于
的面积等于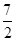 时点
时点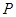 的坐标.
的坐标.
【答案】
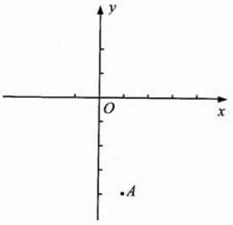
解:(1)由题意,知点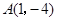 是抛物线的顶点,
是抛物线的顶点,
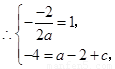
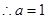 ,
,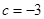 ,
,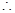 抛物线的函数关系式为
抛物线的函数关系式为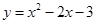 .
.
(2)由(1)知,点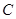 的坐标是
的坐标是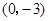 .设直线
.设直线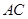 的函数关系式为
的函数关系式为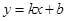 ,
,
则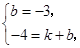
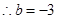 ,
,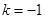 ,
,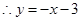 .
.
由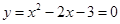 ,得
,得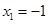 ,
,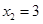 ,
,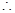 点
点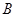 的坐标是
的坐标是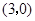 .
.
设直线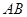 的函数关系式是
的函数关系式是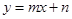 ,
,
则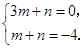 解得
解得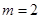 ,
,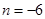 .
.
 直线
直线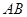 的函数关系式是
的函数关系式是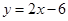 .
.
设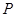 点坐标为
点坐标为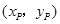 ,则
,则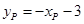 .
.
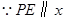 轴,
轴,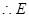 点的纵坐标也是
点的纵坐标也是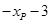 .
.
设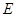 点坐标为
点坐标为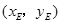 ,
,
 点
点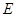 在直线
在直线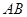 上,
上,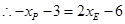 ,
,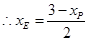 .
.
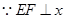 轴,
轴,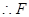 点的坐标为
点的坐标为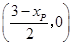 ,
,
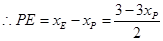 ,
,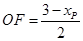 ,
,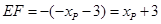 ,
,
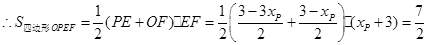 ,
,
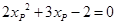 ,
,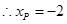 ,
,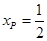 ,当
,当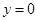 时,
时,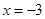 ,
,
而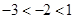 ,
,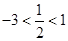 ,
,
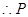 点坐标为
点坐标为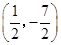 和
和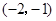 .
.
【解析】(1)由题意可知抛物线的顶点就是A点,因此可将A的坐标代入抛物线的解析式中,并根据对称轴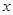 =
=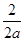 =1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.
=1,联立方程组即可求出a,c的值,进而可得出抛物线的解析式.
(2)四边形OPEF是个直角梯形,可先求出AD,AB所在直线的解析式,根据AD所在直线的解析式设出P的坐标,又由于PE∥x轴,P、E两点的纵坐标相同,然后根据AB所在直线的解析式得出E点的坐标,进而可求出F点的坐标.根据求出的P、E、F三点坐标,可得出梯形的上下底OF、EP的长以及直角梯形的高EF的长(即E点纵坐标的绝对值),根据梯形的面积公式即可得出关于梯形的面积与P点坐标的函数解析式,然后将S=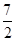 代入函数中即可求出P点的坐标
代入函数中即可求出P点的坐标

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
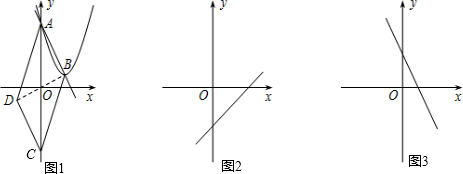
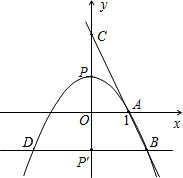 探究线段CA与CB的比值:
探究线段CA与CB的比值:

