题目内容
如图,已知抛物线经过定点A(1,0),它的顶点P是y轴正半轴上的一个动点,P点关于x轴的对称点为P′,过P′作x轴的平行线交抛物线于B、D两点(B点在y轴右侧),直线BA交y轴于C点.按从特殊到一般的规律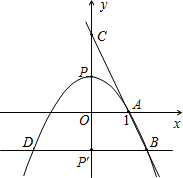 探究线段CA与CB的比值:
探究线段CA与CB的比值:(1)当P点坐标为(0,1)时,写出抛物线的解析式并求线段CA与CB的比值;
(2)若P点坐标为(0,m)时(m为任意正实数),线段CA与CB的比值是否与(1)所求的比值相同?请说明理由.
分析:(1)根据抛物线经过A(1,0),设抛物线的解析式为y=ax2+1,首先得出二次函数解析式,进而得出P'点的坐标,从而得出B点坐标,再利用△CP′B∽△COA,得出线段CA与CB的比值;
(2)根据设抛物线的解析式为y=ax2+m(a≠0),得出y=-mx2+m,首先表示出B点的坐标,进而利用△CP′B∽△COA,得出线段CA与CB的比值.
(2)根据设抛物线的解析式为y=ax2+m(a≠0),得出y=-mx2+m,首先表示出B点的坐标,进而利用△CP′B∽△COA,得出线段CA与CB的比值.
解答:解:(1)设抛物线的解析式为y=ax2+1(a≠0),
∵抛物线经过A(1,0),
∴0=a+1,a=-1,
∴y=-x2+1.
∵P′、P关于x轴对称,且P(0,1),
∴P′点的坐标为(0,-1),
∵P′B∥x轴,
∴B点的纵坐标为-1,
由-1=-x2+1,
解得x=±
,
∴B(
,-1),
∴P'B=
.
∵OA∥P'B,
∴△CP'B∽△COA,
∴
=
=
=
.
(2)设抛物线的解析式为y=ax2+m(a≠0),
∵抛物线经过A(1,0),
∴0=a+m,a=-m,
∴y=-mx2+m.
∵P′B∥x轴,
∴B点的纵坐标为-m,当y=-m时,-mx2+m=-m,
∴m(x2-2)=0,
∵m>0,
∴x2-2=0,
∴x=±
,
∴B(
,-m),
∴P'B=
,
同(1)得
=
=
=
.
∴m为任意正实数时,
=
.
∵抛物线经过A(1,0),
∴0=a+1,a=-1,
∴y=-x2+1.
∵P′、P关于x轴对称,且P(0,1),
∴P′点的坐标为(0,-1),
∵P′B∥x轴,
∴B点的纵坐标为-1,
由-1=-x2+1,
解得x=±
| 2 |
∴B(
| 2 |
∴P'B=
| 2 |
∵OA∥P'B,
∴△CP'B∽△COA,
∴
| CA |
| CB |
| OA |
| P′B |
| 1 | ||
|
| ||
| 2 |
(2)设抛物线的解析式为y=ax2+m(a≠0),
∵抛物线经过A(1,0),
∴0=a+m,a=-m,
∴y=-mx2+m.
∵P′B∥x轴,
∴B点的纵坐标为-m,当y=-m时,-mx2+m=-m,
∴m(x2-2)=0,
∵m>0,
∴x2-2=0,
∴x=±
| 2 |
∴B(
| 2 |
∴P'B=
| 2 |
同(1)得
| CA |
| CB |
| OA |
| P′B |
| 1 | ||
|
| ||
| 2 |
∴m为任意正实数时,
| CA |
| CB |
| ||
| 2 |
点评:此题主要考查了二次函数的综合应用以及相似三角形的性质,得出根据P′B=
,再利用△CP′B∽△COA,得出是解决问题的关键.
| 2 |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
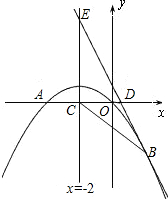
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.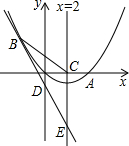 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),