题目内容
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上 
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.
【答案】
(1)证明:选取①②,
∵在△BEO和△DFO中 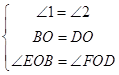 ,
,
∴△BEO≌△DFO(ASA);
(2)证明:由(1)得:△BEO≌△DFO,
∴EO=FO,BO=DO,
∵AE=CF,
∴AO=CO,
∴四边形ABCD是平行四边形.
【解析】(1)选取①②,利用ASA判定△BEO≌△DFO即可;(2)根据△BEO≌△DFO可得EO=FO,BO=DO,再根据等式的性质可得AO=CO,根据两条对角线互相平分的四边形是平行四边形可得结论.
【考点精析】本题主要考查了平行四边形的判定的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

练习册系列答案
相关题目





