题目内容
【题目】如图，在平面直角坐标系中，正方形ABCD的对角线AC，BD交于点E，其中点A(1，1)，B(5，1)，C(5，5)，D(1，5).一个口袋中装有5个完全相同的小球，上面分别标有数字1，2，3，4，5，搅匀后从中摸出一个小球，把球上的数字作为点P的横坐标，放回后再摸出一个小球，将球上数字作为点P的纵坐标，求点P落在阴影部分(含边界)的概率.
【答案】
【解析】试题分析：列举出所有情况，让P点落在阴影部分（含边界）的情况数除以总情况数即为所求的概率．
试题解析：列表得：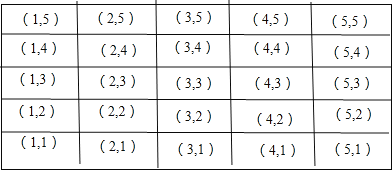
∴共有25种情况，
根据题意：直线AC与BD的解析式为
y=x与y=-x+6
当x=1时，均可；
当x=2时，（2，2）、（2，3）（2，4）可以；
当x=3时，（3，3）可以；
当x=4时，（4，2）、（4，3）、（4，4）可以；
当x=5时，均可；
∴P点落在阴影部分（含边界）的有17种；
∴P点落在阴影部分（含边界）的概率是
．
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案【题目】问题背景：
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”，他觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说：你完成下面的问题后就可能知道该如何简化计算啦！
获取新知：
请你和小红一起完成崔老师提供的问题：
（1）填写下表：
x=﹣1，y=1 | x=1，y=0 | x=3，y=2 | x=1，y=1 | x=5，y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
（2）观察表格，你发现A与B有什么关系？
解决问题：
（3）请结合上述的有关信息，计算4×3.142﹣4×3.14×3.28+3.282．
【题目】一城市准备选购一千株高度大约为2米的某种风景树来进行街道绿化，有四个苗圃基地投标（单株树的价相同），采购小组从四个苗圃中任意抽查了20株树苗的高度，得到表中的数据. 你认为应选( )
树苗平均高度 | 标准差 | |
甲苗圃 | 1.8 | 0.2 |
乙苗圃 | 1.8 | 0.6 |
丙苗圃 | 2.0 | 0.6 |
丁苗圃 | 2.0 | 0.2 |
A. 甲苗圃的树 B. 乙苗圃的树苗 C. 丙苗圃的树苗 D. 丁苗圃的树苗
