题目内容
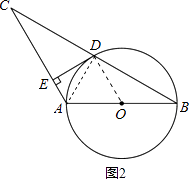
【题目】如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E. 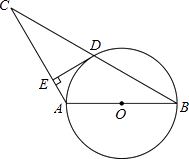
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠C=30°,CE=6,求⊙O的半径.
【答案】
(1)证明:连接OD.
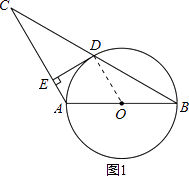
∵D是BC的中点,O是AB的中点,
∴OD∥AC,
∴∠CED=∠ODE.
∵DE⊥AC,
∴∠CED=∠ODE=90°.
∴OD⊥DE,OD是圆的半径,
∴DE是⊙O的切线.
(2)解:连接AD,
∵AB为直径,
∴∠BDA=90°,
∵DE⊥AC,
∴∠CED=90°,
在Rt△CED中,cos∠C= ![]() ,cos30°=
,cos30°= ![]() ,
,
解得:CD=4 ![]() ,
,
∵点D为BC的中点,
∴BD=CD=4 ![]() ,
,
∴AC=AB,
∴∠B=∠C=30°,
在Rt△ABD中.cos∠B= ![]() ,cos30°=
,cos30°= ![]() ,
,
解得AB=8,
故⊙O的半径为4.
【解析】(1)连接OD,只要证明OD⊥DE即可.此题可运用三角形的中位线定理证OD∥AC,因为DE⊥AC,所以OD⊥DE.(2)通过相似三角形的性质或三角函数的定义求出AB或圆的半径的值即可.
【考点精析】利用切线的判定定理和解直角三角形对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目