Question

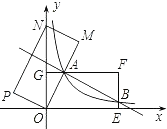
【题目】如图，在平面直角坐标系中，矩形OEFG的顶点F的坐标为（4，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴上，得到矩形OMNP，OM与GF相交于点A．若经过点A的反比例函数 的图象交EF于点B，则点B的坐标为 ．

Answer 1

【答案】（4， ）
【解析】解：∵矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，
∴∠P=∠POM=∠OGF=90°，
∴∠PON+∠PNO=90°，∠GOA+∠PON=90°，
∴∠PNO=∠GOA，
∴△OGA∽△NPO；
∵E点坐标为（4，0），G点坐标为（0，2），
∴OE=4，OG=2，
∴OP=OG=2，PN=GF=OE=4，
∵△OGA∽△NPO，
∴OG：NP=GA：OP，即2：4=GA：2，
∴GA=1，
∴A点坐标为（1，2），
设过点A的反比例函数解析式为y= ，
把A（1，2）代入y= 得k=1×2=2，
∴过点A的反比例函数解析式为y= ；
把x=4代入y= 中得y= ，
∴B点坐标为（4， ）．
所以答案是：（4， ）．