题目内容
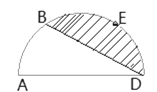
【题目】如图，以AD为直径的半圆经过点E、B，点E、B是半圆的三等分点，弧 BE的长为
，则图中阴影部分的面积为（ ）
A. B. 
C. 
D. 
【答案】D
【解析】分析：如图，连接OB，过O作OF⊥BD于点F，由于B、E是半圆的三等分点，得∠AOB=60°，由弧 BE的长为
可得半圆的半径，故可得扇形的面积，进而求得S△BOD，根据S阴影=S半圆-S扇形AOB- S△BOD即可得解.
详解：如图，连接OB，过O作OF⊥BD于点F，
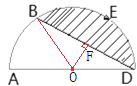
∵点E、B是半圆的三等分点，弧 BE的长为，
∴
∴OA=2
∴
在△BOD中，∠BOD=120°，
∴∠BOF=60°
∴
,
即：OF=BOcos∠BOF=2×
=1
∴BF=
∴BD=2
∴
∴ S阴影=S半圆-S扇形AOB- S△BOD=
=
.
故选D.
练习册系列答案
相关题目
